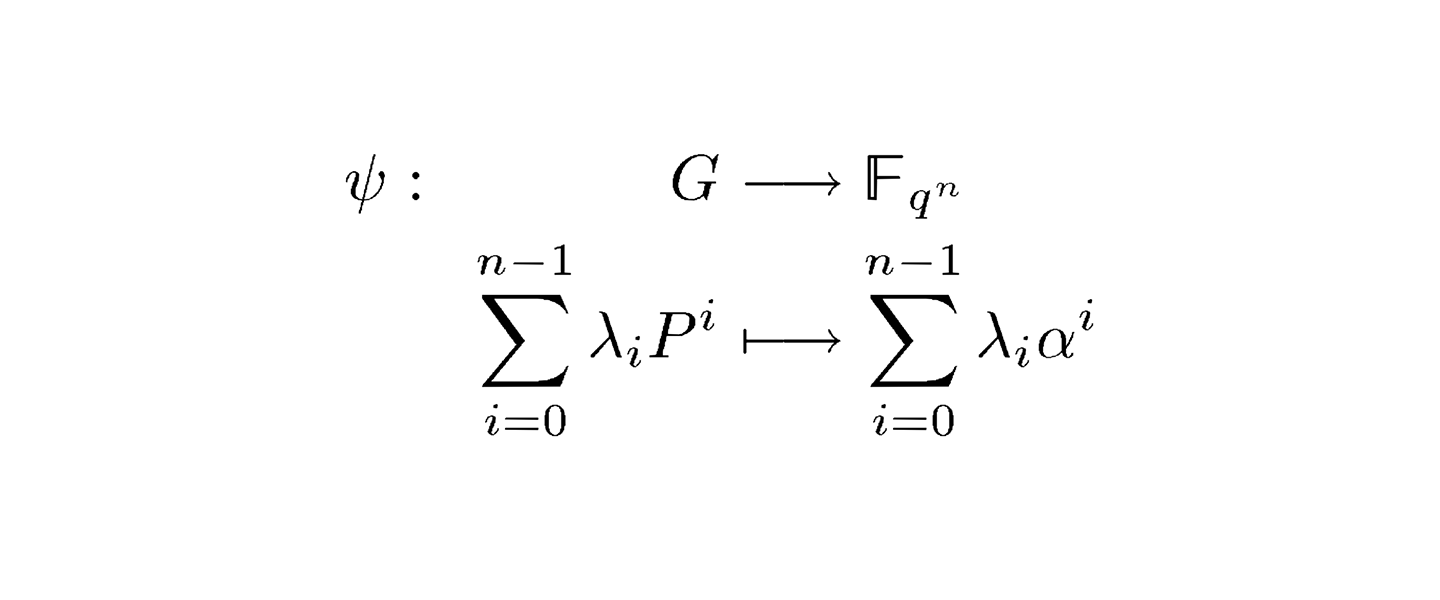ABOUT
PERSONAL DETAILSBIO
ABOUT ME
I am an Associate Professor in the School of Mathematical and Statistical Sciences at Clemson University, where I also serve as the Associate Director for Mathematics and Statistics Education. For the academic year 2019/20 I have been a Visiting Scholar and have since been an affiliated faculty member of the Cybersecurity Research Lab at the Ted Rogers School of Management at Toronto Metropolitan University. I was honored to be a 2019 Simons Visiting Professor and currently serve as an Associate Editor for the IEEE Transaction on Information Theory.