According to my HP48GX one astronomical unit is equal to
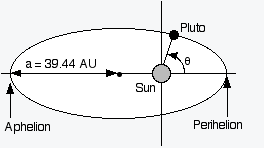
the handout agree. The diagram from the handout is reproduced below.
Kepler and Pluto
MTHSC 108H -- December 11, 1999
From the textbook, p. 695, the orbit of Pluto has a semi-major axis of
![]() km and an eccentricity of 0.2481.
km and an eccentricity of 0.2481.
According to my HP48GX one astronomical unit is equal to
![]() km. Thus the book and the diagrom on
km. Thus the book and the diagrom on
the handout agree. The diagram from the handout is reproduced below.
> 5.900*10^9 / (1.4960*10^8);
![]()
By Kepler's third law the cube of the mean distance to the sun (measured in astronomical units) is
equal to the square of the period (in earth years). Thus we can conclude that the Pluto takes
247.6882 years to complete one orbit of the sun. I have not found any place in the book where it
defines the mean distance to the sun, but it is reasonable to suppose that Kepler and the book mean
that it is the average of the perihelion distance and the aphelion distance. In other words, it is
![]() , the
, the
semi-major axis.
> P := sqrt(39.44^3);
![]()
The polar equation for an ellipse with the orientation of the diagram is
>
assume(0<ecc, ecc<1);
r := theta -> ecc*d/(1 + ecc*cos(theta));
![]()
Now
![]() , so we can relate
, so we can relate
![]() to the given mean distance to the sun.
to the given mean distance to the sun.
>
assume(0<a);
dp := solve(2*a=r(0)+r(Pi),d);
r2 := unapply(subs(d=dp, r(theta)), theta);
![]()
![]()
Personally, I prefer to write this formula as
> r3 := theta -> a*(1-ecc^2)/(1+ecc*cos(theta));
![]()
Now let's look at Pluto specifically.
>
ap := 39.44;
ep := 0.2481;
rp := subs(a=ap, ecc=ep, r3(theta));
pd := evalf(subs(theta=0,rp));
ad := evalf(subs(theta=Pi,rp));
plot(rp,theta=0..2*Pi,coords=polar,title="The Orbit of Pluto",
titlefont=[TIMES,BOLD,14]);
![]()
![]()
![]()
![]()
![]()
![[Maple Plot]](images/Kepler17.gif)
We can determine the area of an ellipse by two different approaches.
We can start with the Cartesian description
![]() , then
, then
set up the area integral for the upper half of the ellipse, and finally make a few simple changes of variable.
> A1 := 2*(b/a)*Int(sqrt(a^2-(x+c)^2),x=-(a+c)..(a-c));
![[Maple Math]](images/Kepler19.gif)
The first change of variable centers the ellipse, and the second and third change are standard trigonometric
substitutions.
>
with(student):
A2 := simplify(changevar(x=u-c,A1,u));
A3 := simplify(changevar(u=a*sin(phi),A2,phi));
A4 := subs(cos(phi)^2=(1+cos(2*phi))/2, A3);
Warning, new definition for D
![[Maple Math]](images/Kepler20.gif)
![[Maple Math]](images/Kepler21.gif)
![[Maple Math]](images/Kepler22.gif)
For the
![]() in the range of
in the range of
![]() to
to
![]() the function
the function
![]() is simply equal to 1. Integrating this gives us
is simply equal to 1. Integrating this gives us
the standard formula for the area of an ellipse. Notice that it reduces to the formula for the area of a circle when
![]() .
.
> ellipseArea := 2*a*b*int((1+cos(2*phi))/2,phi=-Pi/2..Pi/2);
![]()
The second approach is to integrate the ellipse using the area element for polar coordinates.
>
A5 := 2*Int((1/2)*r3(theta)^2,theta=0..Pi);
A6 := simplify(A5);
![[Maple Math]](images/Kepler29.gif)
![[Maple Math]](images/Kepler30.gif)
>
a^2*(1-2*ecc^2+ecc^4) * int(1/(1+2*ecc*cos(theta)+ecc^2*cos(theta)^2), theta = 0 .. Pi);
ellipseArea2 := simplify(%);
![]()
![]()
We can also obtain the distance from the focus to the center of the ellipse by subtracting the perihelion
distance from
![]() . This in turn gives us the semi-minor axis,
. This in turn gives us the semi-minor axis,
![]() , and shows that the area of the ellipse,
, and shows that the area of the ellipse,
![]() ,
,
is the same as the area from the polar formula.
>
c := simplify(a-r3(0));
b := simplify(sqrt(a^2 - c^2));
totalArea := ellipseArea;
![]()
![]()
![]()
We now define the function which returns the area of a sector from
![]() to
to
![]() .
.
> Area := unapply((1/2)*Int(r3(t)^2,t=alpha..beta),(alpha,beta));
![[Maple Math]](images/Kepler41.gif)
Note that the Area function is defined in terms of an unevaluated integral. By using the evalf function
we can construct a function that evaluates this integral numerically. This seems to work much better in
practice, even though this is an elementary integral.
Specializing these formulas to Pluto yields.
>
cp := subs(a=ap, ecc=ep, c);
bp := subs(a=ap, c=cp, ecc=ep, b);
Ap := unapply(evalf(subs(a=ap, ecc=ep, Area(alpha,beta))),(alpha,beta));
![]()
![]()
![[Maple Math]](images/Kepler44.gif)
We are now in a position to solve for the angle that Pluto will be at when it has completed 1/8 of an Pluto year
starting either at the perihelion or at the aphelion. Note that we need to use fsolve, the numerical solve routine.
>
evalf(Pi*ap*bp/8);
t0 := fsolve(Ap(0,theta)=Pi*ap*bp/8,theta);
evalf(Ap(0,t0));
t1 := fsolve(Ap(Pi,theta)=Pi*ap*bp/8,theta);
evalf(Ap(Pi,t1));
evalf(t1-Pi);
timeP := evalf(P/8);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Starting at the perihelion, Pluto sweeps out a sector with an angle of 1.21906 radians or 69.85 degrees and the
area of the sector is 1/8 of the entire area of the ellipse. Similarly, starting at the aphelion, Pluto sweeps out
a sector with an angle of 0.50165 radians or 28.74 degrees. Each sector has the same area, and by Kepler's
Second Law, each sector will be swept out in the same amount of time - about 30.96 earth years.
The distance traveled between 0 and t0 (or Pi and t1) is simply the arclength from 0 to t0 (or Pi to t1).
The arc length integral is
not
an elementary integral. Maple will provide an answer involving the Elliptic
integral functions. It is so involved as to be worthless, and a numerical approach is much simpler.
To see this, simply change Int to int in the definition of
![]() . Scroll through the lengthy result
. Scroll through the lengthy result
and notice the occurence of the special functions EllipticE and EllipticF.
>
dr := diff(r3(theta),theta);
s := Int(sqrt(r3(theta)^2 + dr^2),theta=alpha..beta);
![]()
![[Maple Math]](images/Kepler54.gif)
Specializing to Pluto yields.
> sp := unapply(subs(a=ap, ecc=ep, s), (alpha,beta));
![[Maple Math]](images/Kepler55.gif)
Now we can answer the questions.
>
distance1 := evalf(sp(0,t0));
avgSpeed1 := distance1 / timeP;
![]()
![]()
So we see that starting at the perihelion in
![]() of a Plutonian year or 30.96 earth years, the planet will travel a distance
of a Plutonian year or 30.96 earth years, the planet will travel a distance
of 38.2826 AU at an average speed of 1.2365 AU/year.
>
distance2 := evalf(sp(Pi,t1));
avgSpeed2 := distance2 / timeP;
![]()
![]()
And we see that starting at the aphelion, Pluto only travels a distance of 24.4638 AU at an average speed of 0.7901 AU/year.
To convert to convert to km and km/hour we need the following two conversion factors
>
toKm := 1.4960*10^8;
toKmpH := toKm/(365*24);
![]()
![]()
Thus when starting at the perihelion, Pluto travels
![]() km at an average speed 21,116 km/hour .
km at an average speed 21,116 km/hour .
>
distance1*toKm;
avgSpeed1*toKmpH;
![]()
![]()
When starting at the perihelion, Pluto travels
![]() km at an average speed 13,494 km/hour .
km at an average speed 13,494 km/hour .
>
distance2*toKm;
avgSpeed2*toKmpH;
![]()
![]()
By comparison, if we simply treat the earth's orbit as circular, then the earth travels
![]() AU in one year at an
AU in one year at an
average speed of 107,301 km/hour.
> avgEarthSpeed := evalf(2*Pi*toKmpH);
![]()
By the way, Pluto was not discovered until 1930 by C. W. Tombaugh. (It's existence had been conjectured by
Percival Lowell in 1905.) Hence Kepler was stuck with Mars and its much more circular orbit -- which made
Tycho Brahe's precise measurements even more important.
>