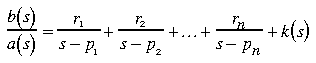
[r,p,k] = residue(b,a)
[b,a] = residue(r,p,k)
[r,p,k] = residue(b,a) find the residues, poles, and direct term of a partial fraction expansion of the ratio of two polynomials, b(s) and a(s). If there are no multiple roots
Vectors b and a specify the coefficients of the polynomials in descending powers of s. The residues are returned in the column vector r, the pole locations in column vector p, and the direct terms in row vector k. The number of poles n is
n = length(a)-1 = length(r) = length(p)
The direct term coefficient vector is empty if length(b) < length(a); otherwise
length(k) = length(b)-length(a)+1
If p(j) = ... = p(j+m-1) is a pole of multiplicity m, then the expansion includes terms of the form
[b,a] = residue(r,p,k), with three input arguments and two output arguments, converts the partial fraction expansion back to the polynomials with coefficients in b and a.
residue is an M-file. It first obtains the poles with roots. Next, if the fraction is nonproper, the direct term k is found using deconv, which performs polynomial long division. Finally, the residues are determined by evaluating the polynomial with individual roots removed. For repeated roots, the M-file resi2 computes the residues at the repeated root locations.
deconv,poly,roots
(c) Copyright 1994 by The MathWorks, Inc.