Cryptosystems Based on Integer Factorization

  Given two primes, say p = 863 and q = 877, it is an easy process to multiply them by hand to get the product n = 756851. However, it is not nearly so easy to determine by hand the factors p and q from only a knowledge of the product 756851. In a similar fashion, if p and q are large, say 1,000 digits each, then a computer can readily find the 2,000 digit product (since multiplying two k-digit numbers requires at most operations), but even the fastest of today's computers cannot generally determine the factors from only the product. This leads us to consider two central problems in the history of mathematics, namely the problems of (a) determining whether a given integer is a prime, and (b) determining the factorization into primes of a given integer. These two problems have been attacked by some of the best mathematicians of all time, including the great C. F. Gauss (1777-1855) who wrote [9]:

The problem of distinguishing prime numbers from composite numbers and of resolving the latter into their prime factors is known to be one of the most important and useful in arithmetic. It has engaged the industry and wisdom of ancient and modern geometers to such an extent that it would be superfluous to discuss the problem at length Further, the dignity of the science itself seems to require solution of a problem so elegant and so celebrated.

Gauss wrote these words some 175 years before primality testing and the integer factorization problem were applied to modern day cryptography, so as important as they were in Gauss' day, they are even more important today.

It is clear from his words that Gauss realized that primality testing was a different problem from that of integer factorization, and since his time, significant progress has been made on both of these problems. For example, there is an efficient probabilistic algorithm called the Rabin-Miller test (see [3, ]) which can recognize a composite number of say 1,000 digits without ever factoring that number, and the primality of a number can also be determined efficiently [1, ]. There have also been developed over the years much improved factoring algorithms [13], but despite this progress, factoring a general composite number with as few as say 200 digits is still out of reach of the fastest computers using the best algorithms known today.

It is not our purpose here to delve into the theory of primality testing and integer factorization (for which we refer the reader to [13, 20] for recent developments). Instead, we simply wish to emphasize that it is easy to generate and multiply large prime numbers but it is not generally possible to factor the resulting answer in reasonable time; that is, integer multiplication appears to be a one-way function. This belief forms the basis for several public-key cryptosystems. We will discuss two of these after reviewing several ideas from modular arithmetic.

Let n be a positive integer and let denote the ring of integers modulo n. It turns out that exponentiation in this ring is easy; i.e., for any and positive integer e, the computation of can be done efficiently. We demonstrate how this is done with an example.
 
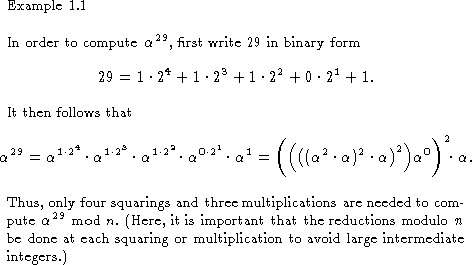
The above idea can be generalized to show that can be computed with squarings and at most multiplications, where is the length of e in its binary representation. So, for any and e>0, can be computed efficiently.

Now consider the reverse of the operation of exponentiation modulo n. Assuming n is specified, two different problems arise: (a) given and , find an integer x (if one exists) such that ; and (b) given e and , find x (if one exists) such that . These two problems are intrinsically different and each of them leads to a public-key cryptosystem.

Problem (a) is called the discrete logarithm problem modulo n and is believed hard for almost all n. (For certain values of n it is easy; e.g., when n has only small prime factors or when n is a prime but n-1 has only small prime factors.) We will discuss this problem and its relation to the ElGamal system in the next section.

Problem (b) asks for the computation of an eth root of an integer y modulo n. This is easy when the complete factorization of n is known but believed hard otherwise. For cryptographic purposes, the most important case is when n is the product of two large (distinct) primes and this is the case we shall develop here. (Our discussion can be readily generalized to the situation where n is square-free.) The RSA system arises when we examine this situation with and the Rabin system comes from considering the case in which e divides . Here is the familiar Euler -function which equals the number of integers in that are relatively prime to n. When n = pq with p and q distinct primes, it is given by .

Assume then that n= pq and let e be an integer with . Then there exists an integer d such that . Using Fermat's little theorem, it is straightforward to show that
 
This means that for any , is an eth root of x modulo n; hence an eth root of x can be computed efficiently provided d is known. Thus an important question is whether d be computed efficiently.

The answer is yes if n can be factored but no otherwise. To explain this statement, first assume that the complete factorization of n into primes is known. Then can be computed quickly. By applying the extended Euclidean algorithm [3] to e and , it is easy to find d such that . Conversely, assume that a number d is known with . Then is a multiple of . By Exercise 9.3, n can be easily factored using . Hence computing d from e and n is equivalent to factoring n. Therefore, the factors of n provide a trap-door for inverting the function defined as

where denotes the smallest nonnegative integer congruent to modulo n.

We can now describe the RSA cryptosystem, which bases its security on the belief that the class of functions are trap-door one-way functions.

We also need a rule for generating a random pair of public and private keys (e,n) and (d,n), but this is not difficult. We have mentioned that primality testing can be done efficiently and further there are many primes with a given number say of t digits (by the prime number theorem). This means that one can generate a t-digit prime as follows. Choose a random number of t digits and test it for primality. If it is not prime, repeat the procedure until a prime is obtained. In this way one can get a pair of primes p and q of any desired size. Then defining n=pq and N=(p-1)(q-1), one may choose a random integer such that . For this e, it is a simple matter to compute d with . Then (e,n) is a public key and (d,n) is the corresponding private key.

We should point out that, even though computing d from e and n is equivalent to factoring n, it has not been proven that inverting is equivalent to computing d or factoring n, as there may exist some other method to compute eth roots modulo n without factoring n or computing d. This raises the following research question.

Open Problem. Given a composite integer n and a positive integer e with , prove or disprove that computing eth roots modulo n is equivalent to factoring n.

We next consider the case in which e divides , used in the Rabin system. Here, the function is no longer a permutation on since for a given e and y, there can be several x that map to the same y under . However, if e is small relative to n, say for some constant c, then it can be proved that finding the inverse images of y under is equivalent to factoring n. Thus, if e is (say) one of 2, 3, 5, 6, 7, then is a candidate trap-door one-way function where the factors of n again provide the trap-door for inverting . Such trap-door one-way functions can be used to build up public-key cryptosystems; indeed, the Rabin system uses only the function and is described as follows.

To decrypt a ciphertext under the Rabin system, we need to describe how to compute square roots modulo n given the factors of n. The idea is to compute square roots modulo each prime factor of n separately and then use the Chinese remainder theorem to combine them to get a square root modulo n. Suppose that has a square root modulo n. Then c also has square roots modulo p and q. Moreover, if r and s are some square roots of c modulo p and q, respectively, and if a and b are integers such that ap+bq=1, then it is easy to check that

is a square root of c modulo n for any choice of + and - signs. This gives four square roots of c. It can be shown that c has exactly four square roots if and only if and c has at least one square root modulo n. To get the correct plaintext one just needs to check which of the roots is in .

It remains to show how to compute square roots modulo a prime p. But this is also easy, especially when , for then is a square root of c whenever c is a quadratic residue in : that is, for some . If p is congruent to 1 modulo 4, square roots modulo p can also be computed efficiently but will not be described here (see [3, 5] for details). Hence computing square roots modulo n=pq is easy when p and q are known.

We conclude this section by showing that if one can compute square roots modulo n then one can actually factor n; that is, we show that computing square roots modulo n is equivalent to factoring n. This also provides a nice example illustrating the power of randomness in computing. Suppose that there is an algorithm which, when presented a quadratic residue , outputs a square root of x in , denoted by . (One may think of as an algorithm, a black box, or an oracle.) Then n can be factored by the following simple algorithm. First, pick a nonzero element uniform randomly and compute . Next, input x to and get . Then compute . It can be shown that for each run of the algorithm, the computed number h is a proper factor of n with probability at least 1/2. If the algorithm is run t times, then the probability of getting a factor of n is at least . Thus for t=10, the chance of finding a factor of n is over ! Therefore n can be factored quickly.

As we have indicated, breaking the Rabin system is equivalent to factoring integers. This is the first example of a public-key cryptosystem with provable security against a passive adversary who can only eavesdrop. Compared to the RSA system, the encryption in Rabin system is more efficient (only one square), and the decryption costs approximately the same as in RSA. However, the same proof above shows that the Rabin system is totally insecure against an active adversary who can mount a chosen ciphertext attack. Under this attack, an adversary chooses some (possibly many) ciphertexts and asks for the corresponding plaintexts, then deduces from them the secret key. The reader should be able to see why this attack works against the Rabin system. Because of this, the Rabin system is not used in practice.