be a finite field of q elements so that 
for some prime
p and integer n. It is well known that the multiplicative group of
nonzero elements of , denoted by 
, is a cyclic group of
order q-1. Thus if 
is a generator of this multiplicative group,
then
every nonzero element 
in is given by 
for
some integer x; in fact for each
there is a unique integer in the range 
with this property.
For a given x and , the power
can be quickly computed by the square-and-multiply
method as demonstrated in Example 9.1.
The inverse problem, i.e., the problem of finding,
for a given and ,
the x in the range 0 < x < q-1 satisfying , is
the discrete logarithm problem; it is believed to be hard for many
fields. Thus, exponentiation in finite fields is a candidate for a one-way
function.
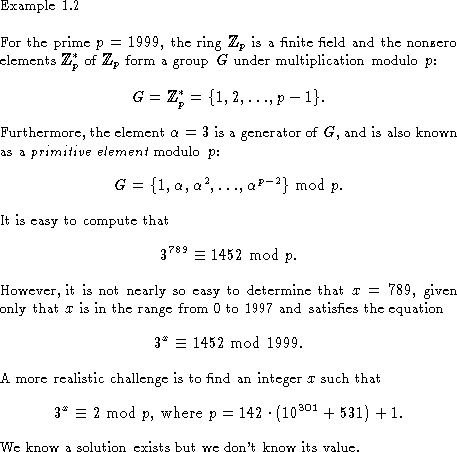
The above discussion can be generalized to any group G (whose operation
is written multiplicatively).
The discrete logarithm problem for G is
to find, for given 
, a nonnegative integer x (if it
exists)
such that .
The smallest such integer x is called the discrete
logarithm of to the base , and is written 
.
In Example 9.2, 
.
Clearly, the discrete logarithm problem for a general group G is exactly
the problem of inverting the exponentiation function
defined by 
where N is the order of
.
The difficulty of this general
discrete logarithm problem depends on the representation
of the group. For example, consider G to be the cyclic group of order
N. If G is represented as the additive group of 
, then computing
discrete logarithms in G
is equivalent to solving the linear equation 
,
where a,b are given integers; this can be easily done by using the
extended Euclidean algorithm.
If G is represented as a subgroup of the multiplicative
group of a finite field as above or as a multiplicative group of elements
from 
(where m may be composite or prime), then the problem can be
``hard.'' For an elliptic curve group [14],
the discrete logarithm problem seems to be harder.
(As we have indicated, no one has been able to
prove that these discrete logarithm problems are really hard, but they have been
studied by number theorists for considerable time with only limited success.)
For recent surveys and a more detailed study of
the discrete logarithm problem, we refer the reader to [15, 18, 19].
We now describe two cryptosystems whose security is based
on the assumption that the discrete logarithm problem is hard.
The Diffie-Hellman key exchange scheme is a protocol for establishing a
common key between two users of a classical cryptosystem.
As we mentioned earlier, for a large network of
users of a conventional cryptosystem, the secure distribution of keys
can be complicated and logistic.
In 1976, Diffie and Hellman [7] gave the following simple and
elegant solution for this problem.
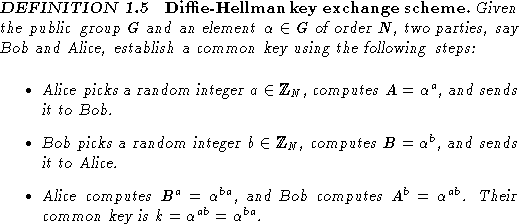
An eavesdropper, who knows G and from the public directory,
after intercepting A and B, is then
faced with the following problem.
If one can solve the discrete logarithm problem, then it is clear that one can solve the Diffie-Hellman problem; hence the latter problem is no harder than the former. It is believed that the two problems are equivalent, and in fact this equivalence has been established for some special cases. In any event, the Diffie-Hellman key exchange scheme is secure provided the Diffie-Hellman problem is hard.
The Diffie-Hellman key exchange scheme is widely used (with some variants)
in practice to generate ``session keys,'' for example in secure internet transactions.
This scheme itself is not a public-key cryptosystem;
however, ElGamal [8] showed that it could easily be
converted into one. Note that if Alice publishes 
but
keeps a secret, then anyone, say Charlie, can share a common key with
Alice in the same way that Bob did; i.e., Charlie can pick a random integer c,
and compute 
and 
.
Before sending r to Alice, Charlie can encrypt any message m
he wishes by simply computing the product 
.
Then he sends the pair 
to Alice.
Alice can compute 
from r and her private key a, and so
decrypt m.
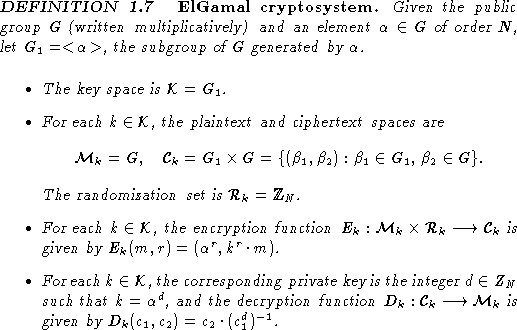
It is easy to check that if 
, then 
and 
.
To obtain a random key, one just chooses 
at random
and computes .
In practice, one has to be extremely careful in choosing the group G so
that the discrete logarithm problem is hard.
Originally, Diffie and Hellman (1976) and ElGamal (1985)
used the multiplicative group of 
for a large prime p.
The above description of their systems
is actually a natural generalization to an arbitrary group.
The most studied groups for cryptographic purposes are multiplicative
subgroups of , (where m is a product of two large primes),
,
and elliptic curve groups over finite fields.
While is currently the most popular choice,
there is increasing interest in using elliptic curves over finite fields,
particularly the fields [14].
Note that breaking the ElGamal cryptosystem by a ciphertext-only attack is equivalent to solving the Diffie-Hellman problem. Thus the ElGamal cryptosystem is another example with provable security if the Diffie-Hellman problem is indeed hard. The major disadvantage of the system is the message expansion by a factor of two, but there are ways to improve it in both efficiency and security as we discuss next.
Observe that the multiplicative operation 
in the encryption
function 
could be replaced by other operations.
For example, if the elements in G are represented as binary strings of
0's and 1's, then we can let
where m is any binary string and 
is the bitwise ``exclusive or'' operation (XOR); e.g.,
. In this case, m does not have to be in G.
If the elements in G are represented as binary strings of
length 
, then the plaintext space 
can be any subset of
binary strings of length .
Note that in the ElGamal cryptosystem, it is required that
a plaintext be in the group. This is not trivial to achieve for some groups
(e.g., elliptic curves), but the above approach solves this problem.
Also, is computationally cheaper than multiplication in a
group.
However, the above alternative does not solve the problem of message expansion.
One way around this is to use 
as a key in a conventional cryptosystem,
say DES or IDEA [12]. That is, define
where 
is any encryption function in a conventional cryptosystem.
Here m can be a message of arbitrary length and operates
on m, say, with cipher block chaining (CBC) mode.
With this modification, the cryptosystem is sometimes called a
hybrid cryptosystem, which combines the advantages of both
public-key and conventional cryptosystems. Such cryptosystems
are practical but do not have provable security (a typical
phenomenon for conventional cryptosystems).
To improve security, one can use a cryptographically strong pseudo-random
bit generator to expand to a much longer string and then
XOR it with m.
It should be noted that the ElGamal cryptosystem is completely insecure against
an adaptive chosen ciphertext attack, mentioned earlier.
Indeed, given an encryption 
of a message m, one can ask for the decryption of 
, which
is 
, so m can be deduced immediately.
