1. Develop an algorithm for computing 
using
the square-and-multiply method indicated in Example 9.1.
Implement your algorithm
and test it for n=12345; 
; and e=0,111, 12344, 54321.
2. Let 
and let e=5. Given that
863 and 877 are primes, find 
and compute d such that
.
3. The following problems relate to the discussion of the RSA system.
,
determine p and q by first determining a quadratic equation
that p satisfies and then solving it using the quadratic formula.
. Write 
where
m is odd.
Prove that for random 
, the probability that
is a proper factor of n for some 
is at least 1/2.
As a consequence, show that n can be factored efficiently when a multiple
of is given.
4. You are an RSA cryptosystem user with
public key n=756851 and e=5. Suppose that a number in
is always written as a 6 digit number (padding zeros in front if
necessary). Then the numbers in represent a triple of letters under the
correspondence 
, 
, 
,
; e.g., 
. Your
private key is the number d computed in Exercise 9.2. Decrypt the
following ciphertext:
5. Suppose that p is a prime congruent to 3 modulo 4 and c is
a quadratic residue modulo p. Prove that
is a square root of c modulo p.
6. Suppose Bob is a Rabin cryptosystem user with public key
n=5609 and private key (p,q)=(71,79). With each
number in representing two letters as
in Exercise 9.4, decrypt the following ciphertext:
7. Investigate how to choose a convenient plaintext space
for Rabin's cryptosystem. That
is, for n=pq, find a subset 
of such that
(a) 
for all different 
;
(b) for any 
, it is easy to decide whether 
;
and (c) should be large, say of size O(n).
8. Decrypt the following ElGamal ciphertexts. The parameters
are p=3119, 
, 
, and d=799. Each number in 
represents two letters as in Exercise 9.4.
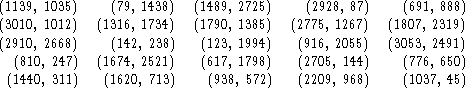
9. Let p=877 and 
. Alice uses the ElGamal signature scheme,
and her public key is 
.
10. Suppose that Bob uses the DSA with q=103,
, 
, a=75, and 
.
Determine Bob's signature on the message x=1001 using the random
value k= 49, and verify the resulting signature.