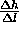 is expanded to be a function of the three space coordinates, x, y, and z. Consequently the velocity v is a vector with components
is expanded to be a function of the three space coordinates, x, y, and z. Consequently the velocity v is a vector with components 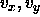 , and
, and 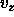 such that the potential head
such that the potential head 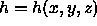 is dependent on the position.
is dependent on the position.
The one dimensional form of Darcy's Law can be generalized to three dimensions such that the head potential, 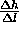 is expanded to be a function of the three space coordinates, x, y, and z. Consequently the velocity v is a vector with components
is expanded to be a function of the three space coordinates, x, y, and z. Consequently the velocity v is a vector with components 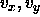 , and
, and 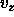 such that the potential head
such that the potential head 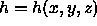 is dependent on the position.
is dependent on the position.
The three dimensional generalization of Darcy's Law, 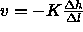 can now be written as:
can now be written as:



Each component takes the partial derivative of h with respect to the corresponding direction, since h is dependent on x, y and z.
Groundwater flow is a function of time and is essentially 3-dimensional in space. The velocity vector at any point has components along three mutually perpendicular axes x, y, and z of a Cartesian coordinate system, thus the velocity is a function of x, y, z and t.
Consider the flow through a small elementary cube whose sides are of length 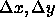 , and
, and 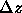 (Figure 2). The law of conservation of matter holds for fluids. Specifically
(Figure 2). The law of conservation of matter holds for fluids. Specifically
The net excess of mass flux, per unit of time, into or out of any infinitesimal volume element in the fluid system is exactly equal to the change per unit of time of the fluid density in the element multiplied by the free volume of the element. [8]Therefore, the sum of the fluid entering the three faces of the cube is equal to the sum of the fluid leaving the cube from the opposite faces plus storage change. The mass inflow in each of the x, y, z directions is:
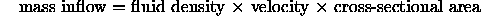
or for each of the specific directions:
mass inflow =

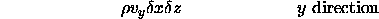
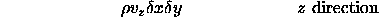
where
since the mass outflow is equal to the mass inflow plus storage change, we have:¯ = fluid velocity (Darcian) in the x, y, z directions respectively [LT
]
= fluid density
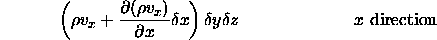
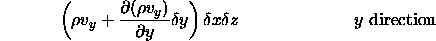
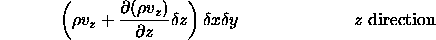
giving the total net inward flux as the sum of differences between the inflow and outflow in each of the three directions.
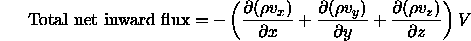
where
V ¯ =Obeying the law of conservation of matter implies this total must equal the change in mass with respect to time:the volume of the cube [L
]
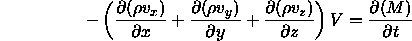
where
M = mass in the elementary cubeEQUATION=
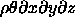
= effective porosity
giving us the Equation of Continuity:
where
Assuming density (= fluid density [ML
]
= fluid velocity (Darcian) in the x, y, z directions respectively [LT
]
= effective porosity
 ) constant and substituting the Darcian velocities(Appendix C) [8]
) constant and substituting the Darcian velocities(Appendix C) [8]

with the specific directions x, y, z in Equation 1 we obtain